[핸즈온머신러닝] Chapter 4. 모델 훈련

4.1 선형 회귀

• 일반적으로 선형 모델은 아래 식처럼 입력 특성의 가중치 합과 편향이라는 상수를 더해 예측을 만듦

• 해당 식을 아래 식처럼 벡터 형태로 더 간단하게 작성 가능

• 회귀에 가장 널리 사용되는 성능 측정 지표는 RMSE(평균 제곱근 오차)
• RMSE를 최소화하는 θ를 찾아야 함
• 실제로 RMSE보다 MSE(평군 제곱 오차)를 최소화하는 것이 같은 결과를 내면서 더 간단

 

   4.1.1 정규방정식

• 비용 함수를 최소화하는  θ값을 찾기 위한 해석적인 방법

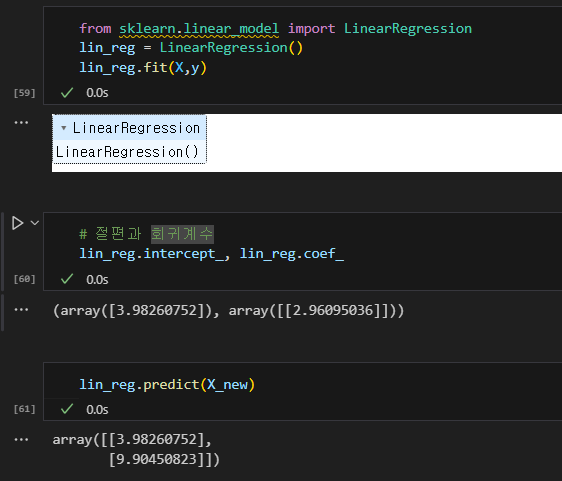
• 사이킷런에서 선형 회귀를 수행하는 것은 간단

 

 

4.2 경사하강법

• Gradient Descent(GD)는 여러 종류의 문제에서 최적의 해법을 찾을 수 있는 일반적인 최적화 알고리즘
• 기본 아이디어는 비용 함수를 최소화하기 위해 반복해서 파라미터를 조정해가는 것

• 파라미터 벡터 θ에 대해 비용 함수의 현재 Gradient를 계산
• θ의 임의의 값으로 시작해서(무작위 초기화) 한 번에 비용 함수가 감소되는 방향으로 진행하여 알고리즘이 최솟값에 수렴할 때까지 점진적으로 향상

 

• 경사 하강법에서 중요한 파라미터 : 학습률 (learning rate)
• 학습률이 너무 작으면 알고리즘이 수렴하기 위해 반복을 많이 진행해야 돼서 시간이 오래 걸림

 

• 학습률이 너무 크면 더 큰 값으로 발산할 수 있음

 

• 경사하강법의 문제점
• 아래 그림에서 알고리즘이 왼쪽에서 시작하면 지역 최솟값(local minimum)에 수렴함
• 오른쪽에서 시작하면 평탄한 지역으로 인해 전역 최솟값(global minimum)에 도달하지 못함

 

• 다행히 선형 회귀를 위한 MSE 비용 함수는 볼록 함수
• 이는 지역 최솟값이 없고 하나의 전역 최솟값만 있다는 뜻
• 또한 연속된 함수이고 기울기가 갑자기 변하지 않음
• 이 두 사실로부터 경사하강법을 통해 전역 최솟값에 가깝게 접근할 수 있다는 것을 보장

   

   중요

• 경사 하강법을 사용할 때는 반드시 모든 특성이 같은 스케일을 갖도록 만들어야 함
• 예를 들어 사이킷런의 StandardScaler를 사용
• 그렇지 않으면 수렴하는 데 훨씬 오래 걸림

 

   

   4.2.1 배치 경사 하강법

• 매 스텝에서 훈련 데이터 전체를 사용
• 속도가 느림

• 학습률 조정
• 왼쪽은 학습률이 너무 낮음. 알고리즘은 최적점에 도달하겠지만 시간이 너무 오래 걸림
• 가운데는 학습률이 적당함. 반복 몇 번 만에 이미 최적점에 수렴
• 오른쪽은 학습률이 너무 높음. 알고리즘이 최적점에서 점점 더 멀어져 발산

 

   4.2.2 확률적 경사 하강법

• 배치 경사 하강법의 가장 큰 문제는 매 스텝에서 전체 훈련 세트를 사용해 gradient 계산
• 훈련 세트가 커지면 매우 느려지게 됨

• 반대로 확률적 경사 하강법은 매 스텝에서 한 개의 샘플을 무작위로 선택하고그 하나의 샘플에 대한 gradient 계산
• 매 반복에서 다뤄야 할 데이터가 매우 적기 때문에 훨씬 빠름

• 반면 확률적이므로 배치 경사 하강법보다 훨씬 불안정
• 비용 함수가 최솟값에 다다를 때까지 위아래로 요동치며 감소
• global minimum에 도달하지 못할 가능성 존재
• 하지만 local minimum에서 탈출하는 데 도움이 됨 

 

• 해당 딜레마를 해결하는 한 가지 방법은 학습률을 점진적으로 감소시키는 것
• 하지만 학습률이 너무 빨리 줄어들면 local minimum에 갇히거나 중간에 멈출 수 있음
• 너무 천천히 줄어들면 오랫동안 최솟값 주변을 맴돌거나 local minimum에 머무를 수 있음

   중요

• 확률적 경사 하강법을 사용할 때 훈련 샘플이 llD(independent and identically distributed)를 만족해야 파라미터가 global minimum에 도달할 가능성이 있음

• IID를 만족하지 못하는 예시로 처음 50장은 고양이, 나머지 5장은 개
• 처음 몇 스텝 동안은 주로 고양이 사진만 무작위로 선택될 확률이 높음
• 결과로 모델은 편향된 학습 결과를 얻게 되어 일반화 성능 X 

• 간단한 해결 방법은 각 epoch를 시작할 때 훈련 세트를 섞는 것

 

   4.2.3 미니배치 경사 하강법

• 미니배치라 부르는 임의의 작은 샘플 세트에 대해 gradient 계산 
• SGD보다 덜 불규칙하게 움직여 최솟값에 더 가까이 도달하게 됨
• 하지만 local minimum에 빠져나오기는 더 힘들지도 모름

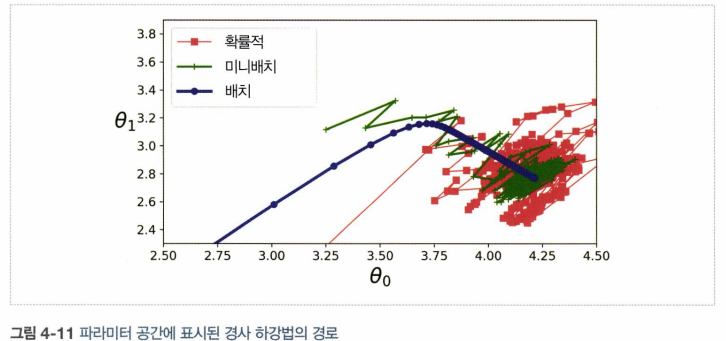
• 배치 경사 하강법은 실제로 최솟값에 멈춘 반면 확률적 경사 하강법과 미니배치 경사 하강법은 근처에서 맴돌고 있음
• 그렇지만 배치 경사 하강법에는 매 스텝에서 많은 시간 소요
• 확률적 경사 하강법과 미니배치 경사 하강법도 적절한 learning rate를 사용하면 최솟값에 도달할 수 있음

 

• m은 훈련 샘플 수, n은 특성 수 
• 해당 알고리즘들은 훈련 결과에 거의 차이가 없음
• 모두 매우 비슷한 모델을 만들고 정확히 같은 방식으로 예측

 

4.3 다항 회귀

• 비선형 데이터를 학습하는 데 선형 모델을 사용할 수 있음

• 우선 2차방정식으로 비선형 데이터 생성

 

• 확실히 직선은 해당 데이터에 잘 맞지 않을 것
• 사이킷런의 PolynomialFeatures를 사용해 훈련 데이터를 변환
• 훈련 세트에 있는 각 특성을 제곱하여 새로운 특성을 추가

 

• Linear Regression 적용

 

 

4.4 학습 곡선

• 고차 다항 회귀를 적용하면 보통의 선형 회귀에서보다 훨씬 더 훈련 데이터에 잘 맞추려고 함
• 아래 고차 다항 회귀 모델은 심각하게 훈련 데이터에 과대적합됨
• 반면 선형 모델은 과소적합, 가장 일반화가 잘된 모델은 2차 다항 회귀
• 2차 방정식으로 생성한 데이터이기 때문에 당연한 결과지만 일반적으로 어떤 함수로 데이터가 생성됐는지 알 수 X

 

• 학습 곡선을 통해 어떤 모델을 사용할지 결정

• 단순 선형 회귀 모델의 학습 곡선
• 과소적합 모델의 전형적인 모습
• 훈련 세트와 검증 세트의 RMSE가 모두 높고 비슷

• 10차 다항 회귀 모델의 학습 곡선
• 훈련 데이터의 오차가 선형 회귀 모델모다 훨씬 낮음
• 두 곡선 사이에 공간이 있음
• 이 말은 훈련 데이터에서의 모델 성능이 검증 데이터에서보다 훨씬 낫다는 뜻이고, 이는 과대적합 모델의 특징
• 그러나 더 큰 훈련 세트를 사용하면 두 곡선이 점점 가까워짐

    중요

• 과대적합 모델을 개선하는 한 가지 방법은 검증 오차가 훈련 오차에 근접할 때까지 더 많은 훈련 데이터를 추가하는 것

 

 

4.5 규제가 있는 선형 모델

• 과대적합을 감소시키는 좋은 방법은 모델을 규제하는 것
• 자유도를 줄이면 데이터에 과대적합되기 더 어려워짐
• 다항 회귀 모델을 규제하는 간단한 방법은 다항식의 차수를 감소시킨는 것

• 선형 회귀 모델에서는 보통 모델의 가중치를 제한함으로써 규제 (릿지, 라쏘, 엘라스틱넷)

 

   4.5.1 릿지 회귀

• 학습 알고리즘을 데이터에 맞추는 것뿐만 아니라 모델의 가중치가 가능한 작게 유지되도록 함
• 규제항은 훈련하는 동안에만 비용 함수에 추가

• 하이퍼파라미터 α는 모델이 얼마나 많이 규제할지 조절
• α=0이면 릿지 회귀는 선형 회귀와 같아짐
• α가 아주 크면 모든 가중치가 거의 0에 가까워지고 결국 데이터의 평균을 지나는 수평선이 됨

• 편향 θ₀는 규제되지 않음
• 릿지 회귀는 입력 특성의 스케일에 민감하기 때문에 수행하기 전에 데이터의 스케일을 맞추는 것이 중요
• 규제가 있는 모델은 대부분 마찬가지

• α를 증가시킬수록 직선에 가까워지는 것을 볼 수 있음
• 즉, 모델의 분산은 줄지만 편향은 커지게 됨

 

 

   4.5.2 라쏘 회귀

• 릿지 회귀처럼 비용 함수에 규제항을 더하지만 가중치 벡터의 L1 노름을 사용

• 라쏘 회귀의 중요한 특징은 덜 중요한 특성의 가중치를 제거하려고 한다는 점 (가중치를 0으로 설정)
• 즉, 필요한 특성만을 사용한 희소 모델 (sparse model)을 만듦

 

   4.5.3 엘라스틱넷

• 릿지 회귀와 라쏘 회귀를 절충한 모델
• 규제항은 릿지와 회귀의 규제항을 단순히 더해서 사용하며, 혼합 정도는 혼합 비율 r을 사용해 조절
• r=0이면 릿지 회귀와 같고, r=1이면 라쏘 회귀와 같음

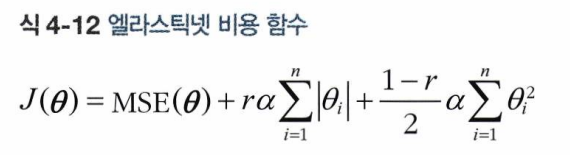
• 릿지가 기본이 되지만 특성이 몇 개뿐이라고 생각되면 라쏘나 엘라스틱 사용 권장
• 해당 모델들은 불필요한 특성의 가중치를 0으로 만들어줌

• 특성 수가 훈련 샘플 수보다 많거나 특성 몇 개가 강하게 연관되어 있을 때는 보통 라쏘가 문제를 일으키므로 라쏘보다는 엘라스틱넷을 선호